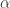ON MIPA PT 2011

Hari Pertama

Soal 1. Misalkan N adalah subgrup berhingga dari grup G. Misalkan G=\langle S \rangle dan N=\langle T \rangle di mana S,T \subseteq G. Buktikan bahwa N normal jika dan hanya jika tSt^{-1} \subseteq N untuk semua t \in T.

(Catatan: Jika X \subseteq G, maka \langle X \rangle = \{x_1x_2 \dots x_k:x_i \in X, k \in \mathbb{N}, \forall i=1,2,\dots,k\}).

Soal 2. (a) Hitunglah

\displaystyle \int_\gamma \frac{\sin(z)}{\cos(z)} dz,

di mana \gamma adalah lengkungan batas kotak -\pi \le \mathrm{Im}(z) \le \pi dan 0 \le \mathrm{Re}(z) \le 2\pi N di mana N adalah bilangan bulat positif.

(b) Hitung juga

\displaystyle \int_\gamma \frac{\sin(z)}{\alpha +\cos(z)}dz,

di mana |\alpha |<1. Periksa semua ketaksamaan yang digunakan!

Soal 3. Diberikan n \in \mathbb{N}, buktikan dengan kombinatorika bahwa

\displaystyle \sum_{k=1}^n k(n+1-k)={n+2 \choose 3}.

Soal 4. Diberikan bahwa S \subseteq \mathbb{R} tertutup dan x \notin S. Buktikan bahwa terdapat y\in S demikian sehingga

|y-x|=\inf(\{|z-x|:z \in S\}).

Soal 5. Misalkan A adalah matriks berukuran n \times n demikian sehingga elemen-elemen pada diagonal utamanya bernilai positif, elemen-elemen lainnya bernilai negatif, dan hasil jumlah semua elemen pada setiap kolom adalah 1. Buktikan bahwa \det(A)>1.

Hari Kedua

Soal 6. Diberikan fungsi f:\mathbb{R} \to \mathbb{R} demikian sehingga untuk setiap \lambda \in [0,1] berlaku f(\lambda x + (1-\lambda)y) \le \lambda f(x) + (1-\lambda)f(y) untuk semua x,y\in \mathbb{R}. Buktikan bahwa

\displaystyle \int_0^{2\pi} f(x) \cos(x) dx \quad \ge 0.

Soal 7. Misalkan V adalah ruang vektor atas real. Fungsi f:V \rightarrow \mathbb{R} memenuhi sifat:

(i) f(\mathbf{v}) \ge 0 untuk semua \mathbf{v} \in V, dan

(ii) [f(\mathbf{u}+\mathbf{w})]^2+[f(\mathbf{u}-\mathbf{w})]^2=2[f(\mathbf{u})]^2+2[f(\mathbf{w})]^2 untuk semua \mathbf{u},\mathbf{w} \in V.

Buktikan bahwa f(\mathbf{u}+\mathbf{w}) \le f(\mathbf{u})+f(\mathbf{w}) untuk semua \mathbf{u}, \mathbf{w} \in V.

Soal 8. Misalkan R adalah ring komutatif dan R[x] adalah himpunan polinomial atas ring R. Untuk suatu polinomial f(x) \in R[x], pandang ring faktor R[x]/\langle f(x)\rangle, dan setiap elemen dari R[x]/\langle f(x)\rangle di tulis sebagai \overline{p(x)} di mana p(x) \in R[x].

(a) Buktikan bahwa jika p(x) dan q(x) dua polinomial berbeda berderajad kurang dari n, maka \overline{p(x)} \neq \overline{q(x)}.

(b) Jika a \in R adalah elemen nilpoten, dan f(x) = x^n-a, maka \overline{x} adalah elemen nilpoten di R[x]/\langle f(x)\rangle.

Soal 9. Diberikan fungsi f:U \to U disebut sebagai biholomorfik jika f memiliki invers, dan f dan f^{-1} keduanya holomorfik atau analitik.

(a) Buktikan bahwa jika U=\mathbb{C}, maka

\displaystyle \lim_{|z| \to \infty} |f(z)| = \infty.

(b) Carilah bentuk umum dari f(z) dan jelaskan argumen Anda.

Soal 10. Misalkan relasi rekuren P_n yang didefinisikan dengan P_1=2 dan P_{n+1}=P_n^2-P_n+1 untuk semua n \in \mathbb{N}. Buktikan bahwa jika m \ne n, maka P_m dan P_n keduanya prima relatif.

Published by

nivotko

truth seeker

3 thoughts on “ON MIPA PT 2011”

  1. ja, solusi2 mu udah hilang ya? kebetulan aku 1,2,3,4,5,6, dan 7 udah selesai, biar digabungin ama solusi mu :D.. Btw, hari pertama no 2 yg b, itu $\latex \alpha$ nya bilangan complex atau real? klo complex jd susah ngitung jumlah pole nya -_- , klo real pake residu langsung trivial.. tp in either case jawabannya sama…

    Reply
  3. Pingback: Some Interesting Property of Convex Function « removablesingularity

Leave a comment