Problem. Show that a triangle is a right triangle if and only if
.
Vietnam 1981
Solution. (By removeablesingularity)
Suppose that
is a a right triangle. Then
. Check that
,
and hence the equation will be satisfied.
Now, suppose that the equation is satisfied. If the left-hand-side (LHS) is squared, we obtain
and if the right-hand-side (RHS) is squared, we obtain.
Recall the trigonometric identities:
(for instance,
)
The equation above after squared then can rewritten as
.
Let us write . Then,
which factorizes to
Hence, or
or
which consecutively implies
,
, or
. Hence, if the equation is satisfied, triangle
has to be a right triangle.
Squaring both sides and a manipulation gives
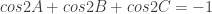
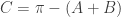 yield
yield 
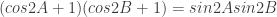 .
.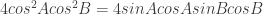 or
or 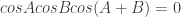 .
.
writing
or
This gives
Mantap Kak. Terima kasih hehe.